Dans ce modèle, l’investissement est défini comme la différence entre le stock de capital désiré (Kt*) et le stock de capital existant (Kt-1) moyennant un coefficient d’ajustement λ (avec o < λ < 1). Mais, pour simplifier notre raisonnement, nous supposons que l’ajustement est immédiat, c’est-à-dire que λ est égal à l’unité.
Le stock de capital désiré, appelé aussi stock de capital optimum est celui qui maximise le profit des entreprises. Le point de départ sera donc la fonction de production de courte période, où le facteur travail sera considéré comme constant, le capital étant le seul facteur variable.
A) LE STOCK DE CAPITAL OPTIMUM
Pour simplifier le raisonnement, nous supposons que le capital est vendu à la fin de la période et racheté ou loué pour la période suivante.
Soit Kt : la quantité de capital détenue par chaque producteur à la fin de la période (t). Le nouveau capital n’étant pas immédiatement opérationnel, nous supposons que ce stock de capital de la période (t) n’entre dans le cycle de production qu’au cours de la période (t+1) :
Yt+1 = f(Kt , Lt+1) (avec L : le niveau de l’emploi).
Etant donné que Lt+1 est donné, l’entrepreneur doit choisir Kt qui maximise Πt+1.
Πt+1 = (Pt+1) (Yt+1) – [(wt+1) (Lt+1) +(cut) (Kt)]
(où w est le coût unitaire du travail et cu le coût unitaire du capital).
Si nous augmentons le stock de capital d’une unité, la production va augmenter de :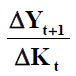
qui n’est rien d’autre que la productivité marginale du capital (PmK) qui, rappelons le, est décroissante lorsque le capital augmente, le niveau de l’emploi restant constant.
Supposons par ailleurs qu’il n’existe qu’un seul bien dans l’économie. Les consommateurs l’achètent pour la consommation, et les producteurs pour l’investissement. Il s’en suit que le prix unitaire du capital à la période (t) est (Pt).
Pour augmenter son capital, le producteur achète une unité de capital au prix (Pt) qui représente le coût en unités monétaires d’une unité d’investissement.
Le rendement de l’investissement est constitué de deux éléments :
- Cet investissement d’une unit é augmente la production Yt+1 de la PmK qui sera vendue au prix Pt+1 c’est-à-dire que le revenu additionnel sera : (Pt+1) (PmK).
- Par ailleurs, tenant compte d’un taux d’amortissement δ, il restera de cet investissement à la fin de la période (1 – δ). Et puisque le producteur vent la totalité de son capital à la fin de chaque période, la valeur résiduelle qui sera récupérée est : (Pt+1) (1 – δ).
Ainsi, une unité d’investissement coûte Pt en t et rapporte en (t+1) : (Pt+1) [PmKt + (1 – δ)]
D’où le rendement en valeur de cet investissement qui correspond au :
Gain net d’une unité d’investissement = Recette marginale + Valeur résiduelle – Prix d’achat
Rappelons par ailleurs que le montant Pt dépensé pour l’achat du capital a un coût d’opportunité, c’est-à-dire un revenu ou un gain qui aurait pu être réalisé si Pt était placé. Si nous supposons que le taux d’intérêt créditeur est égal au taux d’intérêt débiteur (R), nous pouvons dire que :
Le coût d’opportunité des fonds investis = R * Pt
B) LA DECISION D’INVESTISSEMENT
Cette décision dépend de la comparaison entre le gain net (ou rendement de l’investissement) et le coût d’opportunité des fonds investis.
Toute entreprise aura intérêt à augmenter son stock de capital, c’est-à-dire à investir, tant que le rendement du capital est supérieur au coût d’opportunité du capital. Le stock de capital optimum est donc obtenu par l’égalisation entre rendement et coût d’opportunité :
Ceci conduit à deux écritures possibles :
• Soit PmKt – δ = r (2)
Avec PmKt – δ : le taux de rendement réel d’une unité additionnelle d’investissement.
L’équation (2) indique que les investisseurs égalisent le taux de rendement réel de l’investissement et le taux d’intérêt réel.
• Soit PmKt = r + δ (3)
Avec r + δ = cu : le coût d’utilisation du capital pendant une période de production. Ce coût
est appelé coût d’usage du capital.
Selon la relation (3) le capital optimum est obtenu en égalisant ce que rapporte une unité de capital et ce que coûte l’usage de cette unité de capital, c’est-à-dire que le capital optimum est tel que : PmKt = cu.
Et comme il est admis que la production efficace suppose que la productivité marginale est décroissante, alors nous pouvons dire que le stock de capital optimum est une fonction décroissante du coût d’usage du capital.
C) DU STOCK DE CAPITAL OPTIMUM A L’INVESTISSEMENT
Comme Ibt = It + Ατ = (Kt* – Kt-1) + δ Kt-1
Et comme Kt-1 est constante, alors :
C’est-à-dire que l’investissement est en relation décroissante avec le taux d’intérêt nominal et le taux d’amortissement, en relation croissante avec le taux d’inflation anticipé.
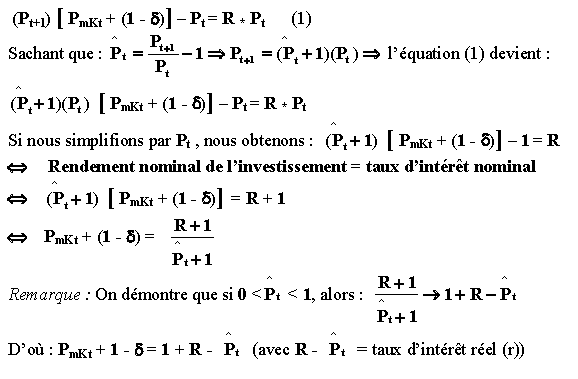
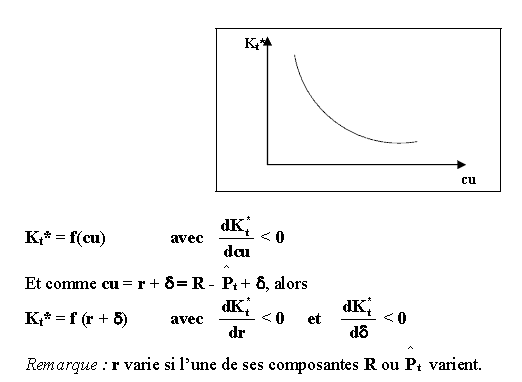
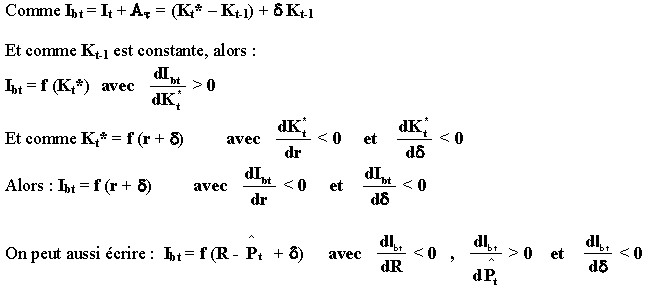
0 commentaires:
Enregistrer un commentaire