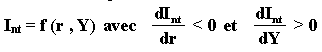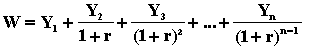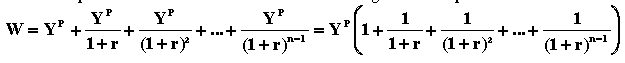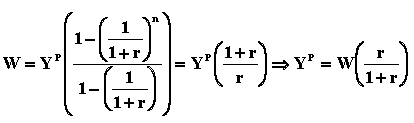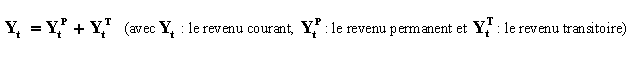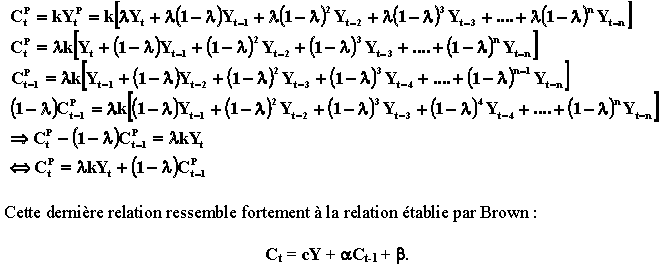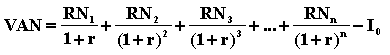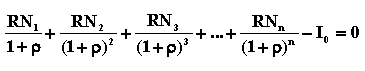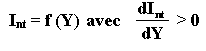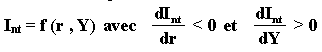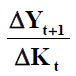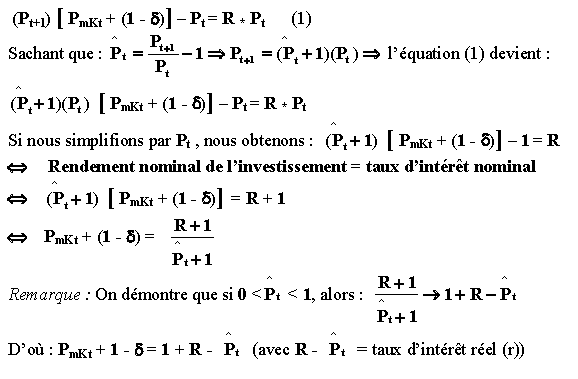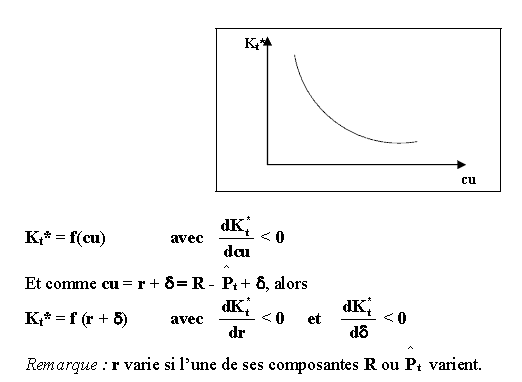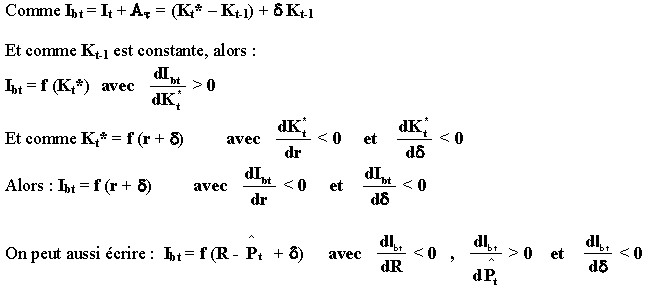l'analyse du comportement de consommateur

 Si nous commençons ce cours de macroéconomie par l’analyse du comportement de consommation, c’est parce que celle-ci revêt une importance capitale en analyse économique en général et en macroéconomie en particulier.

En effet, la consommation est un acte fondateur de l’activité économique dans le sens où c’est elle qui permet de satisfaire nos besoins (individuels et collectifs) et que ces derniers sont à l’origine même de l’activité économique. Ce sont les besoins qui transforme l’être humain passif en agent économique actif.

Par ailleurs, la consommation est en général la composante principale de la demande globale et à ce titre elle est au cœur du débat sur l’efficacité des politiques macroéconomiques de relance. Et c’est pourquoi son étude est un préalable à toute modélisation des politiques économiques.

Ceci étant dit, nous définissons la consommation comme un acte de destruction d’un bien ou d’un service. Cette consommation peut être finale ou intermédiaire. La consommation intermédiaire se rapporte à un bien ou un service qui n’a pas encore achevé son itinéraire dans le processus productif et qui est appelé à être transformé en un autre bien.

Elle correspond donc à une destruction créatrice. Mais la consommation finale est un acte de simple « destruction » destiné à satisfaire un besoin humain.

Cette consommation peut être publique ou privée. Mais dans ce chapitre, nous nous intéressons exclusivement à la consommation privée des ménages. La consommation publique sera considérée comme exogène et intégrée dans les « dépenses publiques ».

 Analyse du comportement de consommation

Notre objectif est de passer en revue les analyses de la consommation globale des ménages en vue de trouver les variables explicatives de cette évolution, c’est-à-dire de dégager ses déterminants.

Le déterminant premier qui a été avancé par les économistes est le revenu. Mais ce concept peut recouvrir diverses réalités : le revenu courant, le revenu relatif ou le revenu permanent.

Keynes retient la notion du revenu courant. Mais d’autres auteurs introduisent certains décalages :

• Duesembery introduit ce décalage au niveau du revenu avec l’hypothèse du revenu relatif : Ct = aYt + bYt-1
• Brown l’introduit au niveau de la consommation pour tenir compte des habitudes : Ct = aYt + bCt-1 + C0.

Ces deux dernières propositions rejoignent celle de Keynes dans la mesure où elles se réfèrent à des facteurs psychologiques.

• A l’opposé de la théorie keynésienne, nous trouvons la théorie du choix inter-temporel proposée par Fisher qui prend en compte le long terme et donc l’évolution de la richesse.

Cette théorie va donner naissance à plusieurs interprétations dont :

• Celle du revenu permanent de Friedman
• Celle du cycle de vie de Modigliani.

Dans ce cours, nous limiterons nos investigations aux propositions de Keynes, Fisher, Modigliani et Friedman.

Fondements et caractéristiques de l'hypothèse du revenu courant

 Selon Keynes, la consommation des ménages s’explique essentiellement par le revenu disponible courant (Yd), c’est-à-dire le revenu national brut net d’impôts et des charges sociales : Yd = Y – T (où Y est le PIB ou le PNB, et T constitue les charges fiscales et parafiscales).

Le point de départ de la théorie keynésienne est une loi dite loi psychologique de Keynes qui s’énonce comme suit : « la loi psychologique fondamentale sur laquelle nous pouvons nous appuyer en toute sécurité, à la fois à priori en raison de notre connaissance de la nature humaine et à posteriori en raison des renseignements détaillés de l’expérience, c’est qu’en moyenne et la plupart du temps, les hommes tendent à accroître leur consommation à mesure que le revenu croît, mais non d’une quantité aussi grande que l’accroissement du revenu ».

De cette proposition, nous retenons que, selon Keynes, la consommation est en relation directe, mais non proportionnelle, avec le niveau du revenu disponible :

(où Ct est la consommation des ménages de la période t).

Par ailleurs, Keynes remarque que même pour un revenu disponible nul, la consommation est positive. Il existe un seuil minimum de consommation qui correspond au minimum vital et qui sera appelé consommation incompressible. Cette remarque et la loi psychologique permettent de formaliser la fonction de consommation keynésienne comme suit :
Ct = C0 + cYdt (où C0 est la consommation incompressible et « c » un paramètre positif inférieur à 1)

De cette relation, nous pouvons tirer un certain nombre de caractéristiques :

• La consommation des ménages comporte deux composantes : une composante autonome (C0) et une composante induite (cYd).
• La propension marginale à consommer, qui mesure la variation de la consommation des ménages conséquente à la variation du revenu disponible d’une unité, est constante et comprise entre zéro et un :
  
• La propension moyenne à consommer, qui mesure la consommation des ménages par unité de revenu disponible, est décroissante et supérieure à la propension marginale à consommer :
  

La PMC décroît de ∞ a c, c’est-à-dire que pour des revenus disponibles très élevés, la PMC tend vers la PmC.

A partir de cette fonction de consommation, nous pouvons déduire celle de l’épargne. En effet, la partie du revenu disponible qui n’est pas consommée sera épargnée, c’est-à-dire que la fonction d’épargne est : St = Ydt – Ct = Ydt – C0 – cYdt = – C0 + (1-c)Ydt = – C0 + sYdt (où St est l’épargne des ménages et s = 1-c).

De cette relation, nous pouvons tirer un certain nombre de caractéristiques :

• L’épargne apparaît comme un résidu.
• La propension marginale à épargner, qui mesure la variation de l’épargne des ménages conséquente à la variation du revenu disponible d’une unité, est constante et comprise entre zéro et un :
  
• La propension moyenne à épargner, qui mesure l’épargne des ménages par unité de revenu disponible, est croissante et inférieure à la propension marginale à épargner :
  La PMS croît de -∞ a s, c’est-à-dire que pour des revenus disponibles très élevés, la PMS tend vers la PmS.
• La somme des propensions marginales à consommer et à épargner est égale à un : PmC + PmS = c + s = c + (1 – c) = 1
• La somme des propensions moyennes à consommer et à épargner est égale à un :
  Représentation graphique:
  
• L’épargne peut être négative ou positive selon le niveau du revenu disponible. Il y a donc un niveau du revenu disponible pour lequel l’épargne est nulle, c’est le seuil d’épargne. Le seuil d’épargne YdE est tel que Remarquons qu’au seuil d’épargne, la propension moyenne à consommer est égale à un et la propension moyenne à épargner est nulle.

Remarque : Les fonctions de consommation et d’épargne définies ci-dessus suggèrent que la somme des propensions marginales à consommer et à épargner est égale à un, mais ne permettent pas de savoir laquelle est supérieure à l’autre. Toutefois, dans une économie « viable », la PmC est nécessairement supérieure à la PmS. Le revenu est destiné essentiellement à la consommation et non à l’épargne.

Exemple :

A partir de cet exemple, nous pouvons constater que :
– La PmC = 0,8 = une constante et la PmE = 0,2 = une constante.
– La PMC est décroissante de ∞ à 0,85.
– La PMS est croissante de – ∞ à 0,85.
– La PMC + PMS =1.
– Le seuil d’épargne est : YdE = 20

Implications et limites de l'hypothèse du revenu courant

 a) Les implications:

• Si nous considérons des ménages à revenus différents, nous observons une PMC de plus en augmente.
• Pour un pays donné, la PMC doit diminuer au fur et à mesure que le niveau de vie de la population s’élève.
• La comparaison entre pays doit faire ressortir une PMC plus faible et une PMS plus élevée pour les pays les plus riches et inversement.

• La consommation est la composante principale de la demande, et de ce fait elle constitue le moteur de la croissance économique. Par conséquent, la baisse de la PMC ne manquerait pas, à terme, de mener les économies qui s’enrichissent vers une stagnation séculaire.

b) Les limites:

La théorie keynésienne de la consommation va être critiquée sur plusieurs flancs.

• La première critique est d’ordre empirique. Nombreux sont les travaux empiriques qui remettent en cause l’hypothèse de Keynes. Mais les travaux les plus significatifs sont ceux menés par Kuznets sur l’économie américaine. Ce dernier livre des résultats contrastés : la thèse de Keynes n’est confirmée qu’à court terme où on observe effectivement une baisse du taux de consommation. Mais les tests empiriques relatifs à des séries historiques révèlent, au contraire, une stabilité du taux de consommation et du taux d’épargne. Par ailleurs, l’histoire concrète n’a pas confirmé la stagnation séculaire qui devrait survenir si l’hypothèse keynésienne était suffisamment robuste.
• La fonction de consommation keynésienne ne tient pas compte de la répartition du revenu. En effet, si nous considérons deux catégories de ménages ayant des fonctions de consommation différentes : les riches avec une PmC faible, et les pauvres avec une PmC élevée. Et étant donnée que la fonction de consommation globale est une agrégation des fonctions de consommation des différentes catégories sociales, alors toute variation au niveau de la répartition des revenus entre riches et pauvres se traduit immanquablement par une modification de la fonction de consommation et donc de la consommation elle-même.
• L’hypothèse du revenu courant ne peut rendre compte du comportement de consommation des ménages dont les revenus subissent des variations aléatoires importantes tels que les exploitants agricoles soumis aux aléas climatiques ou certaines activités soumises à des variations saisonnières importantes. En effet, ces catégories de ménages procèdent souvent à un lissage de leurs revenus en épargnant durant les années « grasses » et en désépargnant durant les années « maigres » comme dans le graphique suivant :
  
  
• La théorie keynésienne donne une explication statique du comportement des ménages dans la mesure où elle ne rend pas compte de l’arbitrage entre la consommation présente et la consommation future et donne à l’épargne un statut de simple résidu. Par ailleurs, il n’ya aucun fondement microéconomique à la formulation macroéconomique du comportement de consommation.

L’ensemble de ces limites rend nécessaire la reformulation de la théorie de la consommation. La contribution de Fisher semble l’alternative la plus exhaustive et celle qui a donné naissance à plusieurs interprétations alternatives.

La théorie du choix intertemporel de Fisher

 La théorie du choix intertemporel de Fisher a été présentée par Irving Fisher en 1930 dans le but de donner un fondement microéconomique à la fonction de consommation macroéconomique. D’inspiration néoclassique, cette théorie suppose des agents rationnels qui agissent dans un environnement de concurrence parfaite. Ces agents raisonnent en terme réel et adoptent un comportement calculateur de maximisation de la fonction objectif sous contrainte.

L’hypothèse de base de cette théorie du choix intertemporel est que la finalité de la consommation des ménages est la maximisation de l’utilité. Mais il ne s’agit pas de maximiser l’utilité pour une période donnée, mais plutôt pour toute la durée de vie. Autrement dit, un ménage serait prêt à sacrifier une certaine quantité de consommation au présent en vue d’avoir une quantité plus élevée au futur et inversement.

Si l’espérance de vie d’un ménage représentatif est de n années, ses revenus disponibles réels annuels anticipés sont : Y1, Y2, Y3, …,Yn, et ses consommations réelles annuelles sont : C1, C2, C3, ……,Cn, alors son plan de consommation intertemporel est celui qui maximise son utilité sous contrainte de richesse.

Le plan de consommation intertemporel

Pour simplifier notre raisonnement, nous supposons un ménage représentatif :

• dont l’espérance de vie est de deux périodes : le présent (période1) et le futur (période 2),
• qui n’a pas de richesse initiale et qui ne lègue rien à ses héritiers.

Supposons que ce ménage a une préférence pour le présent (ρ) c’est-à-dire qu’entre une unité de consommation au présent et la même unité au futur, il préfère consommer au présent. Le taux d’intérêt réel (r) est la récompense de la renonciation au présent, c’est-à-dire la récompense de l’abstinence. Autrement dit, ce ménage obtiendrait (1 + r) unités de consommation au futur s’il accepte de renoncer à une unité de consommation au présent.

Ce ménage peut donc, à chaque période, avoir une consommation inférieure à son revenu courant et épargner le reste ou avoir une consommation supérieure à son revenu courant et emprunter la différence.

Sous ces hypothèses, l’objet de cette section est d’expliquer les mécanismes d’élaboration du plan de consommation intertemporel.

a) La notion de richesse:

Nous désignons par richesse d’un ménage (W), la somme de ses revenus disponibles réels actualisés. L’équation de richesse :

b) La contrainte budgétaire:

Par contrainte budgétaire d’un ménage, nous désignons l’égalité entre ses ressources et leur emploi. Il s’agit, ici, de l’égalité entre la somme de ses revenus disponibles réels actualisés et la somme de ses consommations annuelles réelles actualisées.

Cette dernière relation est l’équation de la contrainte budgétaire ou de richesse. Nous remarquons que c’est une droite décroissante de pente – (1+r).

c) La fonction d’utilité:

L’objectif du ménage représentatif est de maximiser sa fonction d’utilité inter temporelle : U = U( C1 , C2)
Cette fonction peut être représentée, dans un espace à trois dimensions, par une colline d’utilité ou, dans un plan, par une carte d’indifférence qui représente l’ensemble des courbes d’indifférence.

Une courbe d’indifférence intemporelle est le lieu géométrique de toutes les combinaisons de consommation (C1 , C2) qui donnent le même niveau d’utilité.

d) L’optimum:

Maximiser la fonction d’utilité sous la contrainte de richesse revient à maximiser l’équation de Lagrange suivante :

ℑ est maximum lorsque :

Le TMSI (le taux marginal de substitution inter temporel) mesure la quantité de consommation future que le ménage serait prêt de céder pour avoir une unité supplémentaire de consommation présente et garder le niveau d’utilité constant. C’est le taux d’échange subjectif entre la consommation future et la consommation présente.

(1+r) mesure la valeur future d’une unité de consommation présente. C’est le taux d’échange objectif entre la consommation future et la consommation présente. Autrement dit, l’optimum est tel que le taux d’échange objectif est égal au taux d’échange subjectif :

Cet équilibre implique quelques suggestions et remarques :

• Contrairement à l’hypothèse de Keynes, la consommation des ménages ne dépend pas uniquement du revenu disponible, elle dépend également du taux d’intérêt.
• Cet équilibre peut déboucher sur deux catégories de ménages :
  o un ménage créditeur caractérisé par une épargne positive, c’est-à-dire par une consommation présente inférieure au revenu présent : C1* < Y1 ⇔ S > 0.
  o un ménage débiteur caractérisé par une épargne négative, c’est-à-dire par une consommation présente supérieure au revenu présent : C1* > Y1 ⇔ S < 0.
• Comme le ménage considéré ne lègue rien à ses héritiers, sa richesse doit être épuisée à la fin de la deuxième période, c’est-à-dire qu’il ne doit avoir à la fin de sa vie ni une épargne, ni des dettes. Autrement dit son épargne à la deuxième période est égale à moins son épargne de la première période.
  

Déplacement de l’équilibreur

Nous avons montré ci-dessus que la consommation dépend du revenu disponible et du taux d’intérêt, mais nous n’avons pas précisé la nature de la relation (croissante ou décroissante). Pour ce faire, nous devons analyser les conséquences des variations du revenu disponible et du taux d’intérêt, lesquelles variations se traduisent par un déplacement de l’équilibre.

a) variation des revenus disponibles et déplacement de l’équilibre:

Toute variation des revenus disponibles (r restant constant) se traduit par une variation dans le même sens de la richesse. La droite budgétaire va subir un déplacement parallèle, puisque la pente [– (1+r)] ne varie pas, et par conséquent les consommations présentes et futures ainsi que l’épargne vont aussi varier dans le même sens :

b) variation du taux d’intérêt et déplacement de l’équilibre:

Toute variation du taux d’intérêt réel (Y1 et Y2 restant constants) implique un déplacement non parallèle de la droite budgétaire et par la même un déplacement de l’équilibre. Ce déplacement de l’équilibre résulte d’un double effet : un effet substitution et un effet richesse.

• L’effet richesse résulte du fait que le ménage va se sentir plus riche ou plus pauvre selon le sens de variation du taux d’intérêt et selon que l’agent soit débiteur ou créditeur : une augmentation du taux d’intérêt enrichit l’agent créditeur et appauvrit l’agent débiteur et inversement. Et tout enrichissement (appauvrissement) implique une augmentation (une baisse) de C1 et de C2.
• L’autre effet de la variation du taux d’intérêt est la modification de la récompense de la renonciation au présent, c’est à dire du prix de C1 en terme de C2. Ceci se traduit par un effet de substitution qui est le mêmes quelle que soit la situation de l’agent : une augmentation du taux d’intérêt incite à l’épargne et a donc un effet négatif sur la consommation présente et positif sur la consommation future, et inversement.
• Les effets conjugués (effet global) sont donc relativement complexes sur les consommations présentes et futures et sur l’épargne. Ils dépendent du sens de variation du taux d’intérêt et de la situation de l’agent. Toutefois, les tenants de ce modèle font l’hypothèse que lorsque l’effet revenu et l’effet substitution ne vont pas dans le même sens, c’est ce dernier qui l’emporte de sorte que, par exemple, si l’effet revenu est positif et l’effet substitution est négatif, l’effet global sera négatif.

Le tableau suivant récapitule les conséquences des variations du taux d’intérêt réel selon la situation de l’agent.

Remarque : Pour représenter graphiquement l’effet substitution, il faut créer un point intermédiaire en traçant une droite parallèle à la nouvelle droite budgétaire, tangente à la courbe d’indifférence initiale. Le graphique suivant illustre le cas d’une augmentation du taux d’intérêt pour un agent créditeur.

c) Conclusion:

Si nous supposons que l’effet substitution l’emporte sur l’effet revenu, nous pouvons conclure que l’approche de Fisher établit une relation croissante entre la consommation présente et la richesse (la richesse elle-même est fonction croissante des revenus) et décroissante entre la consommation présente et le taux d’intérêt réel.

L'hypothèse du cycle de vie de Modigliani

 Dans les années 1950, Franco Modigliani va se référer aux conclusions du modèle de Fisher de la consommation pour tenter de résoudre l’énigme de la consommation et expliquer la contradiction entre la théorie keynésienne et les faits observés. Comme nous l’avons vu, le modèle de Fisher suppose que la consommation d’une période dépend des revenus de toutes les périodes. L’hypothèse que va poser Modigliani est que le revenu est cyclique, qu’il est variable le long de la vie et que les ménages vont transférer une partie de leurs revenus des années « grasses » vers la consommation des années « maigres ».

L’objectif de ces transferts de revenus est d’avoir une structure de consommation relativement stable durant toute la vie.

La principale raison à l’origine des fluctuations des revenus est l’existence d’une période d’activité où les revenus sont relativement élevés, et d’une période d’inactivité (la retraite) où les revenus sont relativement faibles, voir nuls. Le rôle de l’épargne, dans ce cas, est de répondre au désir des ménages de ne pas voir leur consommation baisser substantiellement durant la période de retraite. Cette incitation à épargner va avoir des implications sur la fonction de consommation.

Pour illustrer la contribution de Modigliani, nous supposons un ménage qui dispose d’une richesse initiale égale à Wo. Ce ménage s’attend à vivre encore n années dont e années d’activité et (n – e) années de retraite. Il perçoit, durant la période d’activité, un revenu annuel constant égal à Y. Il ne lègue rien à ses héritiers.

Question : quel niveau de consommation doit-il avoir pour être en mesure de « lisser » sa consommation durant toute la durée de vie ?
Pour simplifier le raisonnement, nous supposons que le taux d’intérêt est nul.

Les ressources de ce ménages s’élèvent à : Wo + e Y

Sa consommation annuelle sera donc :

Exemple :
pour n = 40 et e = 20, la fonction de consommation est : C = 0,025 W0 + 0,5 Y.

Cette dernière relation indique que la consommation dépend de la richesse et du revenu. Toute unité supplémentaire de richesse implique une augmentation de la consommation de 0,025 unité, et toute augmentation du revenu se traduit par une augmentation de la consommation de 0,5 unité.

Si tous les ménages adoptent un comportement similaire, la fonction de consommation agrégée sera : C = α W + β Y

Où : α = propension marginale à consommer une partie de la richesse
β = propension marginale à consommer une partie du revenu

A priori, nous pouvons supposer que la richesse est constante à court terme. Elle ne varie qu’à long terme suite à l’accumulation de l’épargne.

Au niveau individuel, la richesse augmente, puis baisse. Mais pour l’ensemble des ménages, c’est-à-dire au niveau macroéconomique, la richesse suit un trend ascendant. Ainsi :

• à court α W = α W0 (une constante) et la fonction de consommation est : C = α W0 + β Y. Cette fonction de consommation est similaire à celle de Keynes où α W0 est la consommation autonome et β Y la consommation induite. Et la PMC=(αW0/Y)+β décroissante par rapport au revenu.
• Mais, à long terme, au fur et à mesure que la richesse augmente, la fonction de consommation va se déplacer vers le haut. L’accroissement du revenu va être compensée par l’accroissement de la richesse de sorte que la propension moyenne à consommer va rester constante. En effet, PMC=(αW/Y)+β
  Et comme W et Y vont augmenter en parallèle, rien ne prédispose la PMC à baisser.
  
  

Ainsi, la contribution de Modigliani a établi que la consommation des ménages dépend en partie du revenu courant, mais elle dépend aussi de la richesse. Cette contribution a permis de résoudre la contradiction entre la théorie de la consommation et l’histoire concrète.

Hypothèse du revenu permanent de M. Frideman

 Comme Modigliani et d’autres auteurs, Friedman va fonder son hypothèse sur celle de Fisher et va élaborer un plan de consommation qui dépasse de loin la période courante. Il va avancer les notions de revenu permanent et de consommation permanente. La théorie du choix inter temporel montre que la richesse et le taux d’intérêt sont des variables explicatives de la consommation. Et comme les revenus futurs ne sont pas observables directement mais anticipés, la richesse elle-même est une notion qui sera, selon l’approche du revenu permanent, anticipée.

A) LA NOTION DE REVENU PERMANENT :

Le revenu permanent est défini comme « la somme qu’un consommateur peut consommer en maintenant constante la valeur de son capital ».
Vu sous l’angle des avoirs d’un ménage, le revenu permanent sera considéré comme le reflet des revenus annuels stables sur une longue période dont la valeur présente actualisée est égale à la richesse de ce ménage. Quand un ménage épargne, il ajoute à sa richesse et accroît donc son revenu permanent. C’est pourquoi, nous pouvons dire que ce concept est intimement lié au concept de richesse (W).

Si la richesse s’écrit :

Le revenu permanent serait ce revenu constant à long terme tel que :

C’est une suite géométrique de premier terme 1 et de raison 1/1+r

Mais cette définition théorique du revenu permanent ne permet pas de l’évaluer d’une manière empirique étant donné l’indétermination des revenus futurs et du taux d’intérêt futur. C’est pourquoi Friedman a proposé, pour surmonter cette difficulté, une définition empirique qui se base sur les revenus observés au présent et durant les périodes passées.

L’hypothèse de base est que les revenus courants subissent, d’année en année, des chocs temporaires aléatoires. Le revenu courant est donc formé par deux composantes : une composante permanente et une composante transitoire :

Le revenu permanent est la composante du revenu que les ménages s’attendent à conserver à l’avenir. Il représente donc la partie stable du revenu. Le revenu transitoire est la composante du revenu dont les agents ne prévoient pas le maintien à l’avenir. Il représente la différence à court terme entre le revenu courant et le revenu permanent à long terme.

Si le revenu permanent est le revenu moyen, le revenu transitoire apparaît comme l’écart aléatoire par rapport à cette moyenne. Cet écart peut être positif ou négatif selon que le revenu courant est supérieur ou inférieur au revenu permanent. Ce dernier est une notion continuellement ajustée dans le temps en fonction de l’évolution des revenus courants des ménages. Il peut être estimé à partir d’un processus d’anticipations adaptatives où le revenu permanent d’une période serait égal au revenu permanent de la période précédente qui sera ajusté à la hausse ou à la baisse selon que le revenu transitoire est positif ou négatif.

Supposons un coefficient d’ajustement λ (0 < λ < 1). Tout écart entre le revenu courant Yt et le revenu permanent de la période précédente sera ajouté ou retranché à l’évaluation du revenu permanent dans une proportion égale à λ, c’est-à-dire que si nous considérons que est le revenu transitoire, alors le revenu permanent sera :

Le revenu permanent est donc la moyenne pondérée des revenus courants des périodes précédentes. Les coefficients de pondération sont de plus en plus faibles au fur et à mesure que l’on remonte dans le passé.

B) LA FONCTION DE CONSOMMATION:

L’idée de base de la théorie du revenu permanent est que les ménages orientent leur consommation permanente en fonction de la partie permanente de leur revenu et adoptent un autre comportement face à leur revenu transitoire. Quand les revenus courants augmentent ou baissent temporairement, les ménages ne bouleversent pas complètement leurs habitudes de consommation. S’il s’agit d’une baisse temporaire, ils puisent dans leur épargne accumulée pour financer leurs dépenses normales de consommation ; s’il s’agit d’une augmentation temporaire, ils consacrent à l’épargne une proportion plus élevée de leur revenu que d’habitude.

L’idée maîtresse derrière la théorie du revenu permanent est que la consommation courante est une proportion du revenu disponible courant, mais cette proportion est plus importante pour la partie du revenu qui est permanente et plus faible pour celle qui est transitoire. Les ménages épargnent une plus grande proportion de leur revenu transitoire que celle relative à leur revenu permanent. Si leurs revenus transitoires deviennent négatifs, ils puisent dans leurs épargnes pour maintenir leurs niveaux de vie.

L’une des conséquences de la distinction entre le revenu permanent et le revenu transitoire est la variation de la PMC et de la PmC à court terme par rapport à leurs valeurs de long terme au cours du cycle économique. En effet, en période d’expansion économique, les ménages réalisent des revenus transitoires positifs et importants, ce qui les incite à l’épargne ; leur richesse va donc augmenter. Ils ont un comportement inverse en cas de récession et de
revenus transitoires négatifs.

Deux forces contraires agissent ainsi sur la PMC. La première tend à favoriser une baisse du ratio C/Y à court terme en période d’expansion et une hausse en période de ralentissement.

Cela est dû au fait que la consommation est relativement stable dans le temps, mais les revenus le sont moins. Mais ces tendances sont contrecarrées par la tendance des ménages à épargner une forte proportion des revenus transitoires. La conséquence de ces mécanismes est que la fonction de consommation n’est stable qu’à long terme. A court terme cette fonction est instable.

Ce coefficient est, selon Friedman, proche de l’unité, mais il peut varier d’un pays à l’autre et d’une catégorie de ménages à l’autre. Dans ses études empiriques, l’auteur trouve une valeur égale à 0,88 pour les Etats-Unis.

Pour (k = 0,9) et (λ = 0,25) : la propension marginale à consommer le revenu permanent est égale à 0,9 et la propension marginale à consommer le revenu transitoire est égale à 0,225. Ceci veut dire que l’épargne normale représente 0,1 du revenu permanent et l’épargne spéciale représente 0,775 du revenu transitoire.

Les conclusions de la théorie du revenu permanent de Friedman sont très semblables à celles de la théorie de la consommation en escalier de Duesenberry qui explique la variabilité de la PMC à court terme et sa stabilité à long terme par le fait que les ménages deviennent habitués à un certain niveau de vie et résistent à tout changement brusque de ce dernier.

Par ailleurs, il est également possible d’établir une relation de proximité entre les conclusions de Friedman et celles de Brown. En effet :

Le comportement d’investissement

 L’investissement est l’acte qui consiste à acquérir des biens d’équipement durables destinés à accroître la production de biens et services dans le futur. Les dépenses d’investissement représentent le montant total que :

• les entreprises dépensent pour l’achat d’usines, d’outillages ou d’équipements ou pour le financement des études ;
• les ménages consacrent à l’achat de biens immobiliers neufs ;
• l’Etat consacre aux équipements collectifs

Mais dans ce chapitre, nous nous intéressons uniquement à l’investissement privé, et notamment celui des entreprises. L’investissement public sera intégré dans les dépenses publiques.

Remarques :
– L’acquisition de valeurs mobilières (obligations, actions, …) est exclu. Il s’agit d’un simple transfert d’un élément d’actif (monnaie) vers un autre élément d’actif (actions).
– Le produit de la revente de biens d’équipements ou de biens immobiliers est également exclu. Cet acte représente un simple transfert de propriété et ne constitue en aucun cas un accroissement de la capacité productive de l’économie considéré.
– Il faut distinguer la formation brute de capital fixe (FBCF) de l’investissement (I). En effet :

I = FBCF + ΔSt (où ΔSt est la variation de stock)
– Il faut également distinguer l’investissement brut (Ibt) de l’investissement net (Int).
L’investissement net est égal à l’accroissement du stock de capital, alors que l’investissement brut intègre aussi les investissements de remplacement (les amortissements). Ces derniers servent à maintenir le stock de capital constant suite à sa dépréciation par usure physique ou par usure technologique (obsolescence). Le montant de l’amortissement est difficile à estimer, mais le plus souvent, on suppose qu’il représente une proportion constante du stock de capital de la période précédente. Si nous supposons que le stock de capital (K) se déprécie à un taux constant (δ), nous pouvons écrire :

Ibt = Int + Ατ = (Kt – Kt-1) + δ Kt-1

Rôle de l’investissement:

L’investissement joue un double rôle au sein de l’activité économique :
– En tant que composante de la demande finale globale, l’investissement est, comme la consommation, une dépense et à ce titre, il peut soutenir l’activité économique indépendamment de l’usage concret auquel il est destiné.
– Mais en tant que facteur de production, l’investissement est souvent considéré comme le moteur de la croissance économique dans la mesure où il accroît les capacités productives du pays et améliore sa productivité.

Partant de ces considérations, l’objet de ce chapitre est de déterminer les facteurs explicatifs de l’investissement. Cette tache n’est pas aisée dans la mesure où l’investissement résulte d’un choix relativement complexe où se mêlent des facteurs objectifs observables et mesurables, tel que le taux d’intérêt, et des facteurs subjectifs dont l’évaluation est difficile, telle que la confiance des milieux d’affaire.

Toutefois, tout en reconnaissant l’existence et l’importance de ces derniers facteurs, les économistes ne vont pas leur accorder beaucoup de place et vont mettre en avant, selon les écoles de pensée, un ou deux facteurs explicatifs objectifs. Les classiques se limitent au rôle fondamental du taux d’intérêt et Keynes introduit, en plus, la demande anticipée.

La theorie keynesienne de la demande d’investissement

 La théorie keynésienne de la demande d’investissement:La décision d’investissement est le fait du producteur qui décide de transformer des avoirs monétaires en actifs physiques, c’est-à-dire en biens d’équipement. Cette décision va dépendre, selon Keynes, du taux d’intérêt et du volume des ventes anticipé.

La théorie keynésienne de la demande d’investissement

le rôle du taux d’intérêt dans la décision d’investissement:

Tout investissement doit être financé, soit par des fonds propres, soit par des emprunts. Et dans les deux cas, les intérêts représentent le coût rattaché à cet investissement. Et comme les entrepreneurs cherchent toujours la rentabilité financière, ils vont comparer ce coût avec le rendement du projet. Cette rentabilité peut être étudiée par référence au critère de la Valeur Actuelle Nette.

L’approche de la VAN:

La règle fondamentale en matière de décision d’investissement est celle de la valeur actuelle nette (VAN) qui consiste à comparer le coût et les recettes d’un projet d’investissement.

Lorsqu’un entrepreneur étudie une opportunité d’investissement, il se trouve en présence de deux groupes d’éléments.

• Une dépense d’investissement (I0) à engager immédiatement pour l’acquisition de biens d’équipement dont la durée de vie est de (n) années.
• Des recettes futures nettes (RN) attendues résultant de la vente des produits obtenus grâce à l’investissement considéré sur toute sa durée de vie.

Soit donc RN1, RN2, …, RNn, les recettes nettes attendues, ou les rendements escomptés, par un entrepreneur qui envisage d’acheter des biens d’équipement d’une valeur I0. Soit r le taux d’intérêt et n la durée de vie utile des équipements.

Pour décider de la faisabilité d’un projet, il faut calculer sa VAN, c’est-à-dire la différence entre la somme des revenus actualisés et le coût d’achat des équipements :

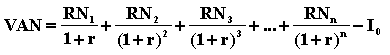
Ce projet ne sera considéré comme rentable et ne sera réalisé que si sa VAN est positive.

Exemple :

I0 = 66085 , n = 3 , RN1 = 36000 , RN2 = 24000 , RN3 = 18000 , r = 0,08.

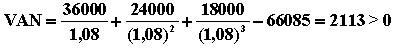
Ce projet est rentable et peut être réalisé du fait que sa VAN est positive.

Le Taux de rendement interne:

Partant de la VAN, Keynes va proposer le concept alternatif d’Efficacité Marginale du Capital (EMC), appelé aussi Taux de Rendement Interne de l’investissement (TRI).

Le TRI est le taux d’actualisation (ρ) qui rend la différence entre la valeur présente de l’investissement et ses revenus futurs égale à zéro. Le TRI d’un projet ρ est tel que :

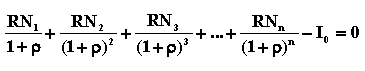
Dans ces conditions, la décision d’investissement va résulter d’une comparaison entre ρ et le taux d’intérêt. Pour qu’un investissement soit réalisé, il faut que son TRI soit supérieur au taux d’intérêt.

Exemple :
Partant du projet décrit dans l’exemple précédent, la solution de la relation :

Autrement dit, ce projet n’est rentable que pour des taux d’intérêt inférieur à 10%.

Partant de cette règle, nous supposons un entrepreneur face à plusieurs projets d’investissement à TRI différents. La démarche à suivre dans ce cas est de (i) classer les différents projets par TRI décroissants, (ii) comparer ces TRI au taux d’intérêt tel qu’il apparaît sur le marché financier, (iii)décider des projets à réaliser selon la règle : ρ > r.

Supposons les 6 projets suivants :

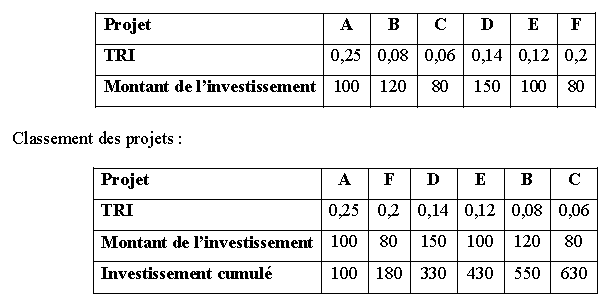
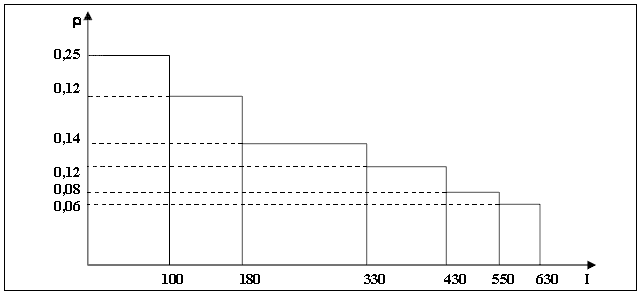
Si r = 5 % : tous les projets seront réalisés et I sera égal à 630.
Si r = 9 % : les projets A, F, D et E seront réalisés et I sera égal à 430.

Ainsi, plus le taux d’intérêt est faible, plus le montant des investissements est élevé du fait qu’il y aura de plus en plus de projets rentables. L’investissement est donc une fonction décroissante du taux d’intérêt : I = f (r) avec dI/dr <0

Remarques :

l’analyse keynésienne de courte période suppose que les prix sont constants, c’est-à-dire que le taux d’inflation anticipée est nul, d’où les taux d’intérêt nominal est réel sont égaux.

à des niveaux très faibles du taux d’intérêt, l’investissement ne dépend plus du taux d’intérêt, c’est-à-dire que la sensibilité de l’investissement au taux d’intérêt sera nulle.

Rôle de la demande anticipée dans la décision d’investissement (la théorie de l’accélérateur)

L’idée de base de cette théorie est que plus l’output sera élevé, plus le capital nécessaire pour le produire est important, et plus donc il faut investir. L’investissement sera donc lié positivement aux variations de la demande anticipée.

Les hypothèses du modèle :

Pour qu’une variation de la demande se traduit par un accroissement des capacités de production, trois conditions, au moins, doivent être vérifiées :

H1 : Les capacités de production sont pleinement utilisées. Il n’y a pas de capitaux oisifs.
H2 : On suppose que la production s’ajuste immédiatement à la demande de sorte que la production remplace la demande dans la fonction d’investissement.
H3 : On suppose une fonction de production à coefficients fixes et des rendements d’échelle constants.

Formulation de l’accélérateur simple :

Si nous supposons que la production s’adapte immédiatement à la demande anticipée, c’est-à dire que : Ya = Y, le principe de l’accélérateur suppose que l’investissement net d’une période est proportionnel à la variation de la production de la même période, c’est-à-dire que :

Kt = α Yt ⇔ Int = α (Δ Yt) = α (Yt – Yt-1)

où α est le coefficient d’accélération, égal au coefficient de capital.
Et comme Yt-1 est une constante, on peut déduire que l’investissement net est une fonction croissante du niveau de production :

 

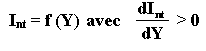
Remarques :

L’investissement nouveau nécessaire pour répondre à l’accroissement de la demande est appelé investissement induit. L’investissement brut sera donc égal à l’investissement induit plus l’investissement de remplacement.

L’accélérateur ne fonctionne que dans le cas où la demande est croissante. Dans le cas où la demande baisse, l’investissement net sera nul et il y aura constitution de capitaux oisifs. En cas d’une reprise de la demande, les capitaux oisifs doivent être utilisés avant de procéder à de nouveaux investissements.

Exemple :
Supposons une entreprise dont le coefficient de capital est égal à 4. A la situation initiale, les capacités de production sont pleinement utilisées. Le taux d’amortissement est égal à 10 %.

La demande anticipée est de 100, 105, 115, 115, 100, 120.
Le tableau suivant illustre le principe de l’accélérateur pour cette entreprise.

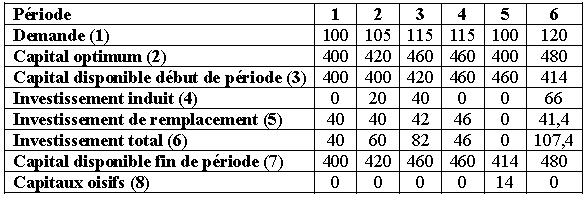
CONCLUSION:

En définitive, la demande d’investissement dans La théorie keynésienne de la demande d’investissement dépend aussi bien du taux d’intérêt que du volume des ventes anticipé.

Le modele neoclassique de l'investissement

 Dans ce modèle, l’investissement est défini comme la différence entre le stock de capital désiré (Kt*) et le stock de capital existant (Kt-1) moyennant un coefficient d’ajustement λ (avec o < λ < 1). Mais, pour simplifier notre raisonnement, nous supposons que l’ajustement est immédiat, c’est-à-dire que λ est égal à l’unité.

Le stock de capital désiré, appelé aussi stock de capital optimum est celui qui maximise le profit des entreprises. Le point de départ sera donc la fonction de production de courte période, où le facteur travail sera considéré comme constant, le capital étant le seul facteur variable.

A) LE STOCK DE CAPITAL OPTIMUM

Pour simplifier le raisonnement, nous supposons que le capital est vendu à la fin de la période et racheté ou loué pour la période suivante.

Soit Kt : la quantité de capital détenue par chaque producteur à la fin de la période (t). Le nouveau capital n’étant pas immédiatement opérationnel, nous supposons que ce stock de capital de la période (t) n’entre dans le cycle de production qu’au cours de la période (t+1) :
Yt+1 = f(Kt , Lt+1) (avec L : le niveau de l’emploi).
Etant donné que Lt+1 est donné, l’entrepreneur doit choisir Kt qui maximise Πt+1.

Πt+1 = (Pt+1) (Yt+1) – [(wt+1) (Lt+1) +(cut) (Kt)]

(où w est le coût unitaire du travail et cu le coût unitaire du capital).

Si nous augmentons le stock de capital d’une unité, la production va augmenter de :qui n’est rien d’autre que la productivité marginale du capital (PmK) qui, rappelons le, est décroissante lorsque le capital augmente, le niveau de l’emploi restant constant.

Supposons par ailleurs qu’il n’existe qu’un seul bien dans l’économie. Les consommateurs l’achètent pour la consommation, et les producteurs pour l’investissement. Il s’en suit que le prix unitaire du capital à la période (t) est (Pt).

Pour augmenter son capital, le producteur achète une unité de capital au prix (Pt) qui représente le coût en unités monétaires d’une unité d’investissement.
Le rendement de l’investissement est constitué de deux éléments :

• Cet investissement d’une unit é augmente la production Yt+1 de la PmK qui sera vendue au prix Pt+1 c’est-à-dire que le revenu additionnel sera : (Pt+1) (PmK).
• Par ailleurs, tenant compte d’un taux d’amortissement δ, il restera de cet investissement à la fin de la période (1 – δ). Et puisque le producteur vent la totalité de son capital à la fin de chaque période, la valeur résiduelle qui sera récupérée est : (Pt+1) (1 – δ).

Ainsi, une unité d’investissement coûte Pt en t et rapporte en (t+1) : (Pt+1) [PmKt + (1 – δ)]
D’où le rendement en valeur de cet investissement qui correspond au :

Gain net = (Pt+1) [ PmKt + (1 – δ)] – Pt

Gain net d’une unité d’investissement = Recette marginale + Valeur résiduelle – Prix d’achat

Rappelons par ailleurs que le montant Pt dépensé pour l’achat du capital a un coût d’opportunité, c’est-à-dire un revenu ou un gain qui aurait pu être réalisé si Pt était placé. Si nous supposons que le taux d’intérêt créditeur est égal au taux d’intérêt débiteur (R), nous pouvons dire que :

 Le coût d’opportunité des fonds investis = R * Pt

B) LA DECISION D’INVESTISSEMENT

Cette décision dépend de la comparaison entre le gain net (ou rendement de l’investissement) et le coût d’opportunité des fonds investis.
Toute entreprise aura intérêt à augmenter son stock de capital, c’est-à-dire à investir, tant que le rendement du capital est supérieur au coût d’opportunité du capital. Le stock de capital optimum est donc obtenu par l’égalisation entre rendement et coût d’opportunité :

Ceci conduit à deux écritures possibles :
• Soit PmKt – δ = r (2)
Avec PmKt – δ : le taux de rendement réel d’une unité additionnelle d’investissement.
L’équation (2) indique que les investisseurs égalisent le taux de rendement réel de l’investissement et le taux d’intérêt réel.
• Soit PmKt = r + δ (3)
Avec r + δ = cu : le coût d’utilisation du capital pendant une période de production. Ce coût
est appelé coût d’usage du capital.
Selon la relation (3) le capital optimum est obtenu en égalisant ce que rapporte une unité de capital et ce que coûte l’usage de cette unité de capital, c’est-à-dire que le capital optimum est tel que : PmKt = cu.

Et comme il est admis que la production efficace suppose que la productivité marginale est décroissante, alors nous pouvons dire que le stock de capital optimum est une fonction décroissante du coût d’usage du capital.

C) DU STOCK DE CAPITAL OPTIMUM A L’INVESTISSEMENT

Comme Ibt = It + Ατ = (Kt* – Kt-1) + δ Kt-1
Et comme Kt-1 est constante, alors :

C’est-à-dire que l’investissement est en relation décroissante avec le taux d’intérêt nominal et le taux d’amortissement, en relation croissante avec le taux d’inflation anticipé.